Hoy continuamos las entradas en las que estoy mostrando cómo implementar en diversos lenguajes de programación el algoritmo que expliqué hace unos días para hallar el Mínimo Común Múltiplo entre dos números enteros positivos (leer aquí el artículo).
Ya lo implementamos en lenguaje Java, y ahora lo haremos en C#, pues como verás son muy similares. De igual forma a como lo hicimos en Java, en esta ocasión también mostraré las dos formas de resolver el algoritmo que se explicaron, es decir, a través del Algoritmo de Euclides y recorriendo cada dígito positivo igual o menor al número menor de entre los cuales se desea hallar el mcm.
Código utilizando el Algoritmo de Euclides:
using System;
namespace MinComMult {
class Program {
/*
* Método para calcular el Máximo Común Divisor
* @param num1: es el primer número ingresado por el usuario
* @param num2: es el segundo número ingresado por el usuario
* @return mcd: es el Máximo Común Divisor entre num1 y num2
*/
public static int mcd(int num1, int num2) {
int mcd = 0;
int a = Math.Max(num1, num2);
int b = Math.Min(num1, num2);
do {
mcd = b;
b = a%b;
a = mcd;
} while(b!=0);
return mcd;
}
/*
* Método para calcular el Mínimo Común Múltiplo
* @param num1: es el primer número ingresado por el usuario
* @param num2: es el segundo número ingresado por el usuario
* @return mcm: es el Mínimo Común Múltiplo entre num1 y num2
*/
public static int mcm(int num1, int num2) {
int mcm = 0;
int a = Math.Max(num1, num2);
int b = Math.Min(num1, num2);
mcm = (a/mcd(a,b))*b;
return mcm;
}
/*
* Método principal
*/
public static void Main(string[] args) {
Console.WriteLine("Ingrese el primer numero");
int num1 = Convert.ToInt32(Console.ReadLine());
Console.WriteLine("Ingrese el segundo numero");
int num2 = Convert.ToInt32(Console.ReadLine());
Console.WriteLine("El M.C.M. entre "+num1+" y "+num2+" es: "+mcm(num1,num2));
Console.ReadKey(true);
}
}
}
Ahora veamos la otra forma que explicamos, que no es más que una variante del Algoritmo de Euclides:
using System;
namespace MinComMult {
class Program {
public static void Main(string[] args) {
// Pedimos los dos números al usuario
Console.WriteLine("Ingrese el primer numero");
int num1 = Convert.ToInt32(Console.ReadLine());
Console.WriteLine("Ingrese el segundo numero");
int num2 = Convert.ToInt32(Console.ReadLine());
// Seleccionamos el menor entre num1 y num2
int min = Math.Min(num1, num2);
// Inicializamos la variable que almacenará el resultado
int mcm = 0;
// Inicializamos el ciclo for encargado
// de realizar las iteraciones
for (int i=1; i<=min; i++) {
// Realizamos la condición que comprobará si el número
// correspondiente a la iteración es el mcd
if (num1%i==0 && num2%i==0) {
// Asignamos el mcd
int mcd = i;
// Calculamos el mcm de forma similar a como se
// hizo utilizando el Algoritmo de Euclides
mcm = (num1*num2)/mcd;
}
}
// Mostramos el resultado en pantalla
Console.WriteLine("El M.C.M. entre "+num1+" y "+num2+" es: "+mcm);
Console.ReadKey(true);
}
}
}
Nuevamente reitero que un código más corto no significa que sea más eficaz que otro más largo, pues como ya pudimos comprobar en las anteriores entradas donde explicamos el Algoritmo para hallar el Mínimo Común Múltiplo, el código más eficaz de éstos dos es el primero al realizar el proceso en menos iteraciones.
Bien, ahora sólo nos resta probar el código y nuevamente lo haremos entonces usando los valores de entrada 12 y 18, a lo cual usando cualquiera de los dos códigos tiene que darnos 36:







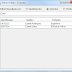
Hola, disculpa no entiendo muy bien que es lo que usted hizo con este código: public static int mcd(int num1, int num2) {
ResponderBorrarint mcd = 0;
int a = Math.Max(num1, num2);
int b = Math.Min(num1, num2);
do {
mcd = b;
b = a%b;
a = mcd;
} while(b!=0);
return mcd;
}
una alternativa es el siguiente, obtenemos el mayor y el menor a través de dos condiciones if y hacemos el ciclo a través de un for, quizás no es el ideal pero para los que estamos empezando a programar y no sabemos que existía el método MAX y MIN:
ResponderBorrarusing System;
public class ejercicio_MCD {
public static void Main() {
//delcaramos nuestras variables.
int numUno, numDos, mayor, menor;
int mcd = 0;
//solicitamos al usuario ingresar dos numeros.
Console.Write("introduce primer numero: ");
numUno = Convert.ToInt32(Console.ReadLine());
Console.Write("introduce segundo numero: ");
numDos = Convert.ToInt32(Console.ReadLine());
//verificamos cual es el numero mayor y cual el menor.
if (numUno > numDos) mayor = numUno;
else
mayor = numDos;
if (numUno < numDos) menor = numUno;
else
menor = numDos;
//entramos al ciclo for.
//i es igual al numero menor mientras i sea distinto a 0 i es igual al numero menor.
for (int i = menor; i != 0; i=menor)
{
mcd = menor;
menor = mayor % menor;
//cada vez que entremos al ciclo menor es igual al residuo de mayor % menor
mayor = mcd;
//mayor es igual a lo que valga mcd cada que entre al ciclo.
}
Console.WriteLine(); //espacio.
//imprime el ultimo valor de mcd cuando i valga cero. (condicion de for)
Console.WriteLine("El M.C.D de {0} y {1} es: {2}",numUno, numDos, mcd);
//pausamos para poder leer en pantalla.
Console.ReadLine();
}
}
una alternativa mas es el siguiente codigo, que muestra MCD y MCM de dos numeros utilizando un while:
ResponderBorrarusing System;
public class MCD_MCM {
public static void Main() {
int numUno, numDos, mayor, menor;
int mcd = 0;
int mcm;
Console.Write("introduce un numero: ");
numUno = Convert.ToInt32(Console.ReadLine());
Console.Write("introduce otro numero: ");
numDos = Convert.ToInt32(Console.ReadLine());
if (numUno > numDos) mayor = numUno;
else
mayor = numDos;
if (numUno < numDos) menor = numUno;
else
menor = numDos;
while (menor!=0) {
mcd = menor;
menor = mayor % menor;
mayor = mcd;
}
mcm = (numUno / mcd) * numDos;
Console.WriteLine("el M.C.D de {0} y {1} es {2} y el M.C.M es {3}",numUno, numDos,mcd,mcm);
Console.ReadLine();
}
}
Gracias por la sugerencia
Borrar